Floyd 算法是解决图论问题的比较经典的算法,用来求解赋权图中每对顶点间的最短距离。当然,在求距离的过程中也可以得到最短距离的路径。这个算法与迪杰斯特拉(Dijkstra)算法相似,他们两个都属于最短路算法,只是Dijkstra算法更适合求图中给定两点的最短距离和路径,求每对顶点之间的距离计算量比较大。不过个人觉得Dijkstra算法更复杂一些,对入门的同学不是很友好。而Floyd 算法相对比较简单,算法容易实现,比较适合入门。
在讲算法之前,兔兔先介绍一下本文用到的图论的相关基础知识。
基础知识
首先是图的表示方法。一般情况下分为关联矩阵、邻接矩阵、邻接表等。其中比较常用的是邻接矩阵,本文先对邻接矩阵做讲解。其次的图的类型。图的类型的非常多的,为了区分比较,本文先介绍相关的4种:无向非赋权图(G),有向非赋权图(D),无向赋权图(G),有向赋权图(D)。关于图论的其它详细知识,兔兔之后会单独在其它文章进行讲解。
对于图,我们可以根据图里面是否有方向(箭头)分为有向图和无向图。有向图,顾名思义就是里面有箭头表示方向,而且只能沿着箭头的方向行走,逆箭头方向就是不能走的,有向图用D表示;无向图,就是双向联通的,没有箭头,在图上用直线连接,通常用G表示。赋权图就是连接两个节点之间的线是有长度的,有具体的数值。非赋权图就是没有长度的要求,更确切的说,就是认为所有长度都用1表示。
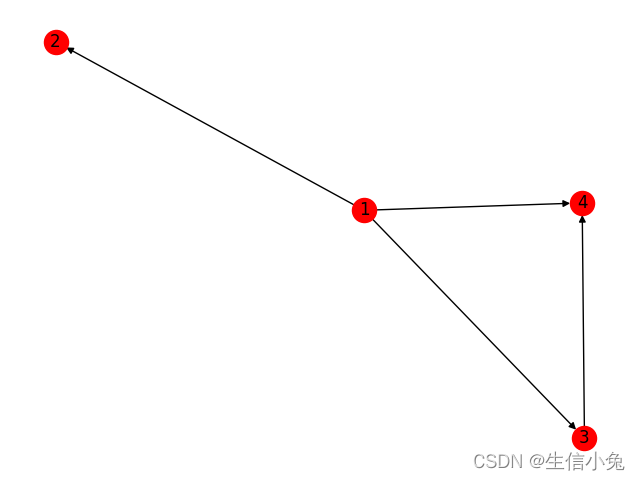
上面的红色是节点,因为有箭头方向,所以是有向图。因为每条线上没有权值,也就是非赋权图。所以可以称为:有向非赋权图。

上面的图就是一个无向图,两个相邻节点是双通的。由于边上有权值,就说明是有长度距离的。比如从1走到2或从2走到1,距离就是3。
在解决最短路问题中,我们遇到的通常是无向赋权图。然后求最短路径。对于上面的图。比如说从3走到2,可以走3->1->2这条路,距离是4+3=7;也可以走3->4->1->2,距离就是3+2+3=8。那么最短路径就是走3->1->2。
求最短路径,我们需要把图转化成数学语言再进行操作,邻接矩阵就是这样的东西。比如上面4个节点1,2,3,4。我们把一个二维矩阵每一个行代表一个节点。第一行是节点1,第二行节点2......然后每一列也代表一个节点,第一列节点1,第二列节点2......这样第i行第j列就代表节点i与节点j之间的距离,也就是权值。如果两个节点之间没有连线(在无向图中),或是在有向图中没有从i指向j的箭头,那就用0或无穷符号表示。在赋权图中矩阵上对应的值是权值,那么在非赋权图中就用0,1表示:1代表连接,0代表没有连接通路。对于对角线元素,就是自己和自己,用0表示。
那么,对于第一个图,邻接矩阵就是:
| 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 |
第二个图,邻接矩阵如下:
| 0 | 3 | 4 | 2 |
| 3 | 0 | 0 | 0 |
| 4 | 0 | 0 | 3 |
| 2 | 0 | 3 | 0 |
不难发现,无向图的邻接矩阵是对称阵。
算法原理
Floyd算法是经典的动态规划算法,基本思想是递推产生一个矩阵序列A1,A2,.....,Ak,...,An(图有n个节点),Ak=(ak(i,j))nxn。其中矩阵Ak第i行第j列表示从顶点vi到顶点vj的路径上经过的顶点序号不大于k的最短路径长度。
迭代公式:
k是迭代次数,i,j,k=1,2......n。
当最后k=n是时,An矩阵就是各个顶点之间的最短距离值了。
那么如果需要记录路径,那么需要引入路由矩阵。路由矩阵Rk=(rk(i,j))nxn,用来记录两点之间路径的前驱后继的关系,其中rk(i,j)表示从顶点vi到顶点vj的路径经过编号为rk(i,j)的顶点。所以需要注意了,路由矩阵里面不是数值,而是结点。
以上理论听起来挺复杂的。不过没有关系的。真正的算法实现无外乎就是三个循环嵌套,i,j的循环是任意两个点,而k则是两个点之间所经过的第三个点,我们就是在循环之中不断比较从i到j的距离与从i到k距离加上从k到j距离的大小,如果经过这个点,路径变短了,我们就接受这个点,认为可以经过这个点;否则就不经过这个点,就是从i到j最短。
如果我们得到的路由矩阵,那怎样得到路径呢?我们得到的路由矩阵Rn,其中r(i,j)(就是路由矩阵第i行j列)表示第i个节点到第j个节点最短路径经过的中间点p1。那么我们先向起始顶点vi反向追踪,得到r(i,p1)=p2,r(i,p2)=p3...,最终r(i,pn)=0,就结束了;再正向追踪,r(p1,j)=q1,r(q1,j)=q2.....r(qt,j)=0,完成正向追踪。路径就是vi,pn,...p2,p1,q1,q2...qt,vj。
算法实现
我们以一个例子来进行算法实现:
import numpy as np
A=np.mat([[0,3,0,2,0],
[3,0,2,1,0],
[0,2,0,0,5],
[2,1,0,0,4],
[0,0,5,4,0]]) #邻接矩阵
G=nx.Graph(A) #无向赋权图
pos=nx.shell_layout(G) #布局设置
w=nx.get_edge_attributes(G,"weight") #获取权重
nx.draw_networkx(G=G,pos=pos,node_size=260) #画网络图
nx.draw_networkx_edge_labels(G=G,pos=pos,font_size=12,edge_labels=w) #标注权重
plt.show()矩阵如下所示:
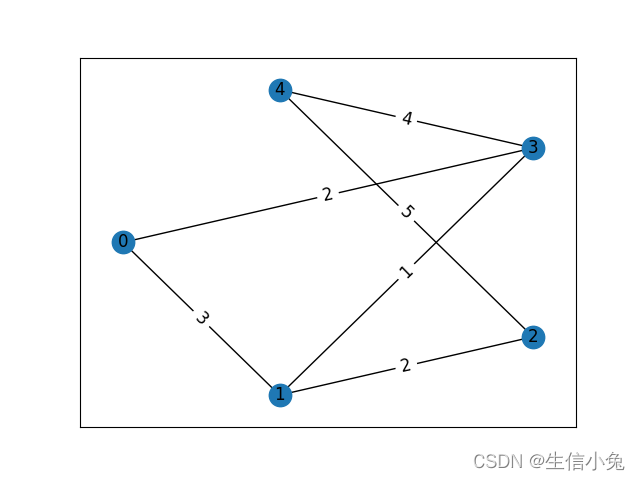
算法代码如下:
import numpy as np
from numpy import inf
A=[[inf,3,inf,2,inf],
[3,inf,2,1,inf],
[inf,2,inf,inf,5],
[2,1,inf,inf,4],
[inf,inf,5,4,inf]]
dis=A #邻接矩阵包含了任意两个节点之间的距离,distance
path=np.zeros((n,n)) #初始化路由矩阵,让它都是零
for k in range(n):
for i in range(n):
for j in range(n):
if dis[i][k]+dis[k][j]<dis[i][j]:
dis[i][j]=dis[i][k]+dis[j][k] #找到经过k点时路径更短,接受这个更短的路径长度
path[i][j]=k #路由矩阵记录路径
print(dis) #显示每对顶点最短路径长度
print(path) #显示路由矩阵为什么这里用inf呢?之前说了,如果两点没有连接或是同一个节点,可以用0或正无穷表示。但是在计算该算法时,如果用零的话,计算过程肯定认为 0 是最短路径,这样我们最终得到的最短路径距离矩阵就是全零矩阵了。所以一定要用inf来表示没有连接的两个节点。
运行结果如下:
dis=[[4, 3, 5, 2, 6],
[3, 2, 2, 1, 5],
[5, 2, 4, 3, 5],
[2, 1, 3, 2, 4],
[6, 5, 5, 4, 8]] #距离矩阵
path=[[3. 0. 1. 0. 3.]
[0. 3. 0. 0. 3.]
[1. 0. 1. 1. 0.]
[0. 0. 1. 1. 0.]
[3. 3. 0. 0. 3.]] #路由矩阵我们以0到4 点为例,最短距离是6。path[0][4]=3,该路径经过点3,反向追踪:path[0][3]=0,结束;正向追踪:path[3][4]=0,结束。最短路径就是0->3->4。看一看前面的图,的确符合事实。
但是,实际上,这五个点最好用a,b,c,d,e等表示,或是1,2,3,4,5。这里的用做终止追踪的0其实是初始时的0,而这个矩阵当中也有作为节点标记的0,看的时候很容易混淆。如果我们用字母标记,最终会看到路由矩阵中有节点标记,也有数字0,看起来会方便很大的。
总结
弗洛伊德算法的算法实现比较简单,过程容易理解,但原理不是很容易消化透彻。同学们在学习的时候可以根据算法过程,找一个具体的图仔细捋一捋,画一下距离矩阵与路由矩阵变化过程,以及当中第三点的选取、距离的比较等,体会当中的动态规划思想。该算法可以求最短路径及其长度,但是对于复杂的网络,该算法还是有局限性的。这个时候我们便需要选择其它的自然算法,例如蚁群算法等来进行求解。虽然那些相对“高级”的算法不一定在众多的路径中找到最短的那一条,但是却可以在较短时间内找到比较短的一条路径,而且会很接近最短路径的。

